Balok adalah salah satu elemen struktur bangunan yang berfungsi utama untuk menerima beban lentur dan geser, namun tidak untuk gaya aksial. Perlu diberi penegasan untuk hal ini, bahwa elemen balok pada Sap2000 memang “benar-benar” tidak dirancang untuk menerima beban aksial sama sekali. Dengan kata lain, efek dari pemberian gaya aksial pada elemen balok Sap2000 akan diabaikan begitu saja alias tidak memberikan efek apapun pada hasil penulangan ataupun perhitungan keamanannya. Oleh karenanya dalam proses permodelan struktur Sap2000, kita harus menentukan terlebih dahulu apakah suatu elemen struktur beton akan kita modelkan sebagai elemen balok atau akan kita modelkan sebagai sebagai elemen kolom. Jangan sampai tertukar atau menganggap (balok dan kolom) akan menghasilkan output penulangan yang sama.
Cara menentukan suatu elemen struktur sebagai balok atau kolom ini dapat kita lakukan dengan cara meng-klik: “Define -> Frame Section -> Add New Property -> Concrete -> Rectangular (untuk beton dengan bentuk penampang persegi)”. Maka akan keluar mini-window seperti di bawah:
Selanjutnya, klik “Concrete Reinforcement”, maka akan muncul window “Reinforcement Data” sebagai berikut:
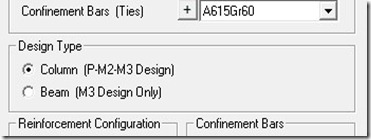
Terlihat secara default, Sap2000 pada awalnya selalu mengkondisikan elemen beton sebagai struktur kolom (mungkin ini adalah option yang paling aman). Sehingga untuk merubahnya sebagai struktur balok , kita hanya perlu merubah design type menjadi “Beam (M3 Design Only)”
Perhatikan baik2 bahwa Sap2000 telah memberikan peringatan yang jelas kepada kita tentang perbedaan antara tipe desain struktur balok dan kolom. Pada “Design Type” berupa kolom tertulis informasi “P-M2-M3 Design”, sedangkan pada struktur balok tertulis informasi “M3 Design Only”.
Loh, bagaimana dengan momen pada sumbu lemahnya (M2)? Apakah selain gaya aksial, momen M2 ini juga tidak diperhitungkan dalam desain balok?
Ya, ternyata dalam Sap2000, elemen balok tidak dirancang untuk menerima gaya pada sumbu lemahnya. Gaya yang dikenakan pada sumbu lemahnya (yang mengakibatkan momen M2) tidak memiliki efek apapun pada hasil output penulangan. Sehingga tentu saja kita tidak bisa mendapatkan hasil penulangan kolom yang benar dengan menentukan type elemen sebagai balok.
Kan sama2 punya tulangan, mas? Kolom bertulang seperti balok juga bisa memikul gaya aksial dan momen sekaligus, kan?
Benar, tentu bisa seperti itu. Balok pun jika ingin dikondisikan sebagai kolom (dianalisis ulang kekuatannya terhadap kombinasi beban P dan M) tentu saja memiliki kekuatan sebagai kolom, asalkan perlu dipahami bahwa beban rencananya-pun tidak sama dengan beban rencana balok murni. Ini berkaitan dengan reduksi kekuatan aksial kolom akibat beban momen. Reduksi kekuatan tekan kolom akibat momen ini dapat jelas terlihat pada grafik Interaksi P-M Kolom. Perhatikan diagram interaksi P-M kolom di bawah:
Terlihat bahwa kekuatan aksial kolom akan berkurang seiring bertambahnya beban momen, hingga pada batas tertentu, kekuatan tekan kolom akan sama dengan 0 kN ketika kolom menerima beban berupa beban momen rencana balok murni. Padahal sudah kita ketahui bahwa penulangan utama balok (secara umum) hanya didesain berdasarkan beban momen rencana (momen ultimate / momen runtuh) saja tanpa memperhitungkan gaya aksial. Sehingga jika beban momen rencana ini tetap terjadi ketika balok berubah fungsi menjadi kolom (dengan konfigurasi penulangan yang sama seperti balok), maka “secara perhitungan”, kolom ini dianggap tidak memiliki tahanan aksial sama sekali.
Jika kita cermati dengan baik, ada dua hal yang menarik dari grafik P-M Kolom di atas. Yaitu sebagai berikut:
a. Dari kondisi P = 0 kN hingga tercapai kondisi “keruntuhan balance” (dimana regangan tekan beton sebesar 0.003 terjadi bersamaan dengan regangan leleh tulangan baja-nya), gaya aksial ternyata akan memberikan kekuatan tambahan pada tahanan momen-nya (konsep balok pre-stress/pra-tegang terjadi). Namun di atas garis “keruntuhan balance”, penambahan gaya aksial justru akan mengurangi kemampuan tahanan momen kolom.
b. Di bawah garis putus-putus horizontal yang menunjukkan keadaan 0.1 fc’Ag (batas atas beban aksial diamana suatu elemen masih dapat didesain sebagai struktur balok), kurva P-M seakan-akan mengalami patahan sehingga bentuk kurvanya menjadi “bengkok”. Ini terjadi karena modifikasi nilai faktor reduksi dari faktor reduksi struktur balok (SNI = 0.8) menuju faktor reduksi struktur kolom (SNI = 0.7 untuk sengkang spiral, 0.65 untuk sengkang persegi).
Belum lagi desain struktur kolom yang benar perlu memperhitungkan stabilitas karena faktor kelangsingan. Desain balok sama sekali tidak memperhitungkan faktor kelangsingan yang berpengaruh terhadap pembesaran momen ini. Sehingga, sekali lagi, jangan dianggap sama ya. :-)
Di bawah saya akan mencoba memverifikasi hasil output penulangan balok Sap2000 dengan perhitungan manual sesuai rumus-rumus umum yang standard kita dapatkan di bangku kuliah maupun dari buku-buku beton. Jika dibandingkan, desain manual balok beton bisa dikatakan jauh lebih mudah dibandingkan dengan desain manual balok baja. Berbeda dengan desain balok baja, dalam mendesain struktur balok beton kita tidak perlu mengecek stabilitas lokal seperti tekuk web/flange maupun efek tekuk torsi lateral. Tentu saja itu karena bentuk penampang struktur beton (baik balok maupun kolom) adalah bentuk pejal yang memiliki perbandingan ketebalan lebar dan tinggi yang cukup besar (jika dalam struktur baja bisa dikatakan termasuk penampang yang super/sangat kompak gitu lah.he2). Sedangkan stabilitas terhadap tekuk torsi lateral tidak perlu ditinjau karena selain alasan di atas (kemungkinan terjadinya tekuk torsi lateral sangat kecil), rata-rata struktur balok beton juga memiliki pengaku lateral di sepanjang bentang berupa slab beton yang berfungsi sebagai lantai bangunan. Sehingga, parameter yang berpengaruh terhadap keamanannya pun cukup sedikit dibandingkan dengan struktur baja. Ini terlihat dari parameter desain yang ditampilkan oleh Sap2000 seperti di bawah.
Berikut adalah desain parameter yang menentukan kekuatan struktur beton (baik balok maupun kolom) pada Sap2000:
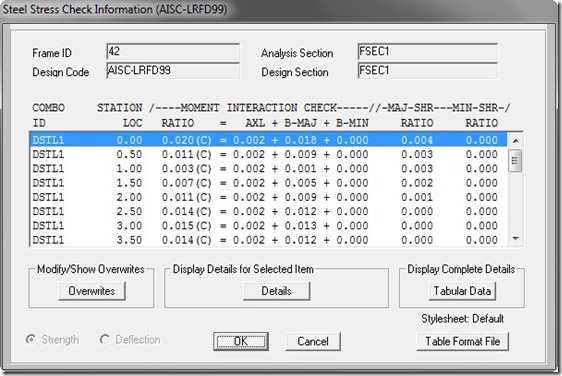
Sedangkan desain parameter yang menentukan kekuatan struktur baja adalah sebagai berikut (selain option pengecekan defleksi):
Wow.. sangat banyak sekali parameter yang perlu diperhatikan dalam mendesain struktur baja ya.. <:-)
Namun dalam mendesain struktur baja dengan Sap2000 kita tidak perlu menentukan suatu elemen adalah termasuk struktur balok atau kolom, karena semua elemen struktur baja akan diperhitungkan sebagai struktur balok dan kolom sekaligus, alias semua aspek desain akan diperhitungkan, baik akibat beban aksial, momen, maupun geser. Maka tidak heran jika kita akan selalu melihat hasil output desain struktur baja (baik itu berupa elemen kolom, balok, maupun bracing sekalipun) adalah berupa stress ratio akumulasi antara stress ratio akibat beban aksial (P), momen (M), dan geser (V) seperti terlihat di bawah:
Oke, langsung saja kita mulai lakukan proses verifikasi.
Untuk proses verifikasi ini akan saya gunakan permodelan balok dengan dimensi tinggi kali lebar (H x B) sebesar 400 mm x 300 mm, dengan lebar bentang 6 m dan bertumpuan sendi-rol (struktur statis tertentu). Input bentuk penampang dan permodelan Sap-nya akan terlihat sebagai berikut:
Perhatikan pada option “Concrete Cover to Longitudinal Rebar Center” (saya singkat menjadi CCL), nilai yang dimasukkan di sini sangat berpengaruh terhadap hasil output desain nantinya (jumlah luas tulangan yang dihasilkan) karena nilai ini akan menentukan besarnya lengan momen antara gaya tekan beton dan gaya tarik tulangan baja-nya.
Secara default, Sap2000 akan memberikan nilai CCL ini sebesar 60 mm. Sebenarnya nilai aktual besaran ini sangat bergantung dari penjumlahan antara tebal selimut beton, diameter tulangan utama, dan diameter sengkang yang digunakan (lihat gambar di bawah).
Jika tebal selimut beton adalah 40 mm (diatur di SNI 03-2847-2002 Pasal 9.7), diameter sengkang adalah 10 mm, dan diameter tulangan utama adalah 25 mm, maka nilai CCL aktual = 40 mm + 10 mm + 0.5(25 mm) = 62.5 mm > 60 mm. Ternyata nilai 60 mm untuk kondisi ini tidak valid. Tentu saja perbedaan nilai ini akan menghasilkan luas tulangan yang juga berbeda, karena semakin kecil lengan momen kopel yang terbentuk maka akan semakin besar luas tulangan yang dibutuhkan (karena semakin besar gaya tarik yang dipikul oleh tulangan). Sehingga nilai CCL = 60 mm (secara perhitungan) hanya valid dan aman untuk tulangan yang sama atau lebih kecil dari tulangan sengkang diameter 10 mm dan tulangan utama berdiameter 19 mm.
Lanjut, lalu pada struktur simple beam ini akan saya kenakan beban mati merata sebesar 10 kN/m seperti capture gambar di bawah:
Sehingga “load case”-nya hanyalah dua beban seperti berikut saja (tidak perlu rumit-rumit agar mempermudah proses verifikasi):
SW (Self Weight) adalah beban sendiri struktur sedangkan DL adalah beban mati selain beban sendiri struktur. Karena keduanya adalah sama-sama beban mati, maka kombinasi beban yang menentukan adalah 1.4 (SW+DL) ( = DCON 1) -> SNI 03-2847-2002 Pasal 11.2.1. Dan berikut adalah data properti material yang digunakan untuk material beton dan tulangannya:
Perhatikan, isian yang saya tandai kotak merah adalah variabel yang perlu diperhatikan dalam perhitungan manual agar nilainya harus sama dengan nilai yang di-input pada Sap.
Sebelum mendesain kebutuhan luas tulangan, perlu diketahui terlebih dahulu reaksi momen yang dihasilkan. Secara perhitungan manual, reaksi momen dari bentuk beban merata di atas dapat kita peroleh dari perhitungan sederhana seperti berikut:
Sedangkan berdasarkan hasil perhitungan Sap2000, reaksi momennya adalah sebagai berikut:
Hasilnya adalah sama, Mu = 81.144 kN.m.
Setelah mengetahui reaksi momen ini, kita dapat langsung menghitung kebutuhan luas tulangan utamanya. Perhitungannya juga sangat simpel, yaitu sebagai berikut:
Sedangkan berdasarkan hasil perhitungan Sap2000 (dengan menggunakan desain peraturan ACI318-99), luas tulangan yang dibutuhkan adalah sebagai berikut:
Dan hasilnya ternyata sama persis (As = 700.694 mm^2).
Atau jika masih penasaran apakah luas tulangan yang digunakan benar2 menimbulkan tahanan momen sebesar ØMn = 81.144 kN.m, kita dapat mengecek langsung dengan rumus analisis sederhana di bawah:
Yup, terbukti, luas tulangan utama yang dihasilkan oleh Sap2000 sesuai dengan rumus manual yang biasa kita gunakan. Lalu bagaimana dengan tulangan minimumnya? Berdasarkan perhitungan manual, tulangan minimum untuk balok 300x400, fc’ = 30 Mpa, dan fy = 400 MPa adalah sebagai berikut:
Catatan: Untuk komponen struktur yang besar dan masif (dimana dengan menggunakan rumus luas tulangan minimum di atas maka akan menghasilkan tulangan minimum yang sangat boros (tahanan momen yang dihasilkan dari jumlah tulangan minimum jauh melebihi beban momen ultimate yang dipikul)), maka rumus tulangan minimum di atas dapat diabaikan dengan syarat seperti yang disebutkan dalam SNI-03-2847-2002, Pasal 12.5.3 (As min = 1/3. As perlu)
Sedangkan Sap2000 menghasilkan luas tulangan minimum sebagai berikut:
Nilainya tidak sama, namun mendekati (luas tulangan minimum Sap 98.49% dari perhitungan manual). Dengan kata lain, perhitungan manual menghasilkan luas tulangan yang lebih “aman” (karena lebih besar nilainya).
Kalau tulangan yang dipasang lebih kecil dari luasan ini gimana mas? Gpp?
Eits, diusahakan jangan. Tulangan tarik diusahakan jangan lebih kecil dari nilai luas minimum ini. Kenapa? Selain berguna untuk tulangan susut (mencegah retak akibat susut beton), pemasangan tulangan minimum ini (yang lebih penting) adalah berguna untuk mencegah keruntuhan getas (keruntuhan tiba-tiba tanpa peringatan). Dalam pelajaran ilmu beton pernah kita dengar bahwa tulangan baja dibutuhkan untuk menahan gaya tarik yang terjadi pada sisi tarik beton karena beton “dianggap” tidak memiliki kekuatan tarik. Tetapi sebenarnya beton memiliki kekuatan tarik, walaupun terbilang sangat rendah (dibanding kuat tekannya). Walaupun kuat tarik beton sangat rendah, namun beton tetap memiliki tahanan terhadap beban tarik tanpa menimbulkan retak pada permukaannya. Bukti simpelnya, silahkan anda tarik beton cetak murni dengan kekuatan tangan anda. Apakah mudah membuatnya terputus/pecah? Tentu tidak, bahkan kekuatan maksimal tangan manusia akan sangat sulit untuk memecahkan beton dengan tarikan. Namun, berapa besar nilai kuat tariknya? Nilai kuat tariknya dapat kita dapatkan dari rumus tegangan retak beton berikut: fcr = 0.7√fc’ MPa. (SNI 03-2847-2002 Pasal 11.5.3(14))
Karena kita telah mengetahui batas tegangan retaknya (fcr), maka momen retaknya pun dapat dengan mudah kita ketahui melalui hubungan antara tegangan retak dengan nilai modulus elastis penampangnya (lihat penjelasannya di sini). Untuk kasus balok 300.400 ini, maka nilai momen retaknya (beserta beban merata minimumnya) yang dapat menimbulkan retak pada beton adalah seperti perhitungan di bawah:
Sedangkan jika kita hitung tahanan momen akibat tulangan minimum, maka hasilnya adalah sebagai berikut:
Bandingkan hasilnya. Tahanan momen retak adalah Mcr = 30.67 kN.m, sedangkan tahanan momen karena tulangan minimum adalah ØMnmin = 42.49 kN.m. Sehingga ketika beban di atas beban retak ini terjadi pada suatu balok beton dengan tulangan minimum, beton tidak akan runtuh tiba-tiba, tetapi sebelumnya akan memberikan peringatan berupa retak terlebih dahulu pada sisi tariknya. Bayangkan jika tahanan momen tulangan minimum ini lebih rendah daripada tahanan momen retaknya, maka ketika terjadi beban yang melebihi beban retak, maka balok akan runtuh secara tiba-tiba (tanpa peringatan).
Namun ada hal yang menarik di sini adalah Sap2000 secara otomatis akan menambahkan tulangan atas (menjadi balok tulangan rangkap) ketika jumlah tulangan tunggal tidak cukup untuk menahan beban momen ultimate yang terjadi. Untuk mengecek hal ini, sebelumnya kita perlu mencari tahu terlebih dahulu berapa luas maksimum tulangan tunggal balok beton agar dapat diketahui berapa besar beban yang akan menimbulkan tulangan atas (tulangan tekan).
Berdasarkan rumus manual, luas tulangan maksimum dapat dicari dengan rumus berikut:
Didapatkan Asmax tulangan tunggal adalah sebesar 2487.206 mm2.
(Hati-hati bahwa rumus rho balance di atas hanya berlaku untuk unit satuan tegangan berupa MPa ( = N/mm2) karena nilai 600 diperoleh dari hasil perkalian antara regangan beton tekan maksimum (0.003) dikalikan dengan modulus elastis tulangan baja (200.000 MPa)).
Setelah mengetahui luas tulangan maksimum, maka dengan membalik perhitungan, dapat kita peroleh beban yang menyebabkan luas tulangan maksimum tersebut. Perhitungannya adalah sebagai berikut:
Maka didapatkan beban merata untuk menimbulkan tulangan tarik maksimum adalah sebesar q = 36.201 kN/m. Untuk menghasilkan tulangan atas kita hanya perlu menaikkan beban merata di atas nilai ini. Untuk pengecekan akan kita gunakan beban merata sebesar q = 37 kN/m ( > 36.201 kN/m).
Jika dihitung manual, maka reaksi momennya adalah sebagai berikut:
Dan Sap2000 juga akan menghasilkan nilai yang sama:
Setelah proses desain kembali dilakukan, maka diperoleh luas tulangan sebagai berikut:
Terlihat Sap2000 secara otomatis memang akan menambahkan tulangan atas ketika luas tulangan bawah maksimun tidak cukup untuk menahan beban momen yang terjadi. Permasalahannya, apakah nilai tulangan maksimum yang didapat antara hitungan manual dengan nilai yang dihasilkan oleh Sap2000 itu sama? Jika dilakukan penyelidikan (dengan proses coba-coba memberikan beban hingga limit tulangan atas mulai akan terbentuk, karena Sap2000 tidak memberikan informasi berapa nilai As maksimum yang digunakan), tulangan maksimum yang diperoleh oleh Sap2000 adalah disekitar nilai 2433.33 mm2. Nilai ini diperoleh dengan memberikan beban merata pada balok sebesar q = 35.55 kN/m (di atas beban ini tulangan atas akan terbentuk). Sedangkan dari perhitungan manual, diperoleh nilai Asmax sebesar 2487.206 mm2 (dari beban q = 36.201 kN/m), lebih besar 2.167 % dari hasil Sap2000.
Rumus desain keperluan tulangan tarik seperti yang digunakan sebelumnya (secara konsep) sudah tidak bisa kita gunakan lagi (walaupun jika ingin digunakanpun hasilnya tidak akan berbeda jauh), karena rumus desain tulangan tunggal yang digunakan sebelumnya hanya berlaku untuk mendesain kebutuhan luas tulangan tarik berdasarkan nilai lengan momen sebesar (d-a/2). Sedangkan untuk mendesain kebutuhan tulangan atas, digunakan nilai lengan momen sebesar (d-60 mm) dimana nilai 60 mm adalah jarak antara pusat tulangan tekan ke tepi beton bagian atas (ingat, nilai ini bisa berubah-ubah tergantung tebal selimut beton dan diameter tulangan yang digunakan). Karena perbedaan nilai antara (d-a/2) dengan (d-60mm) secara umum tidaklah terlalu besar (tidak signifikan), maka jika ingin mendapatkan luas tulangan tarik (dari tulangan rangkap) dengan rumus tulangan tunggal pun hasilnya tidak akan berbeda jauh.
Berikut adalah perhitungan pengecekan tahanan momen tulangan rangkap yang dihasilkan oleh Sap2000. “Dianggap tulangan tekan telah mengalami leleh”. Sehingga perhitungannya adalah seperti berikut:
Kok hasilnya agak berbeda mas?
Perhitungan tahanan momen diatas adalah dengan mengasumsikan tulangan tekan sudah dalam kondisi leleh. Tapi ada kemungkinan tulangan tekan belum mengalami leleh. Maka perlu dicek regangan tulangan atasnya, apakah sudah mencapai regangan leleh atau belum. Jika belum, maka nilai tegangan yang digunakan untuk tulangan tekan adalah sebesar (εs/εy).fy, dimana εs adalah regangan tulangan tekan aktual dan εy adalah regangan tulangan dalam kondisi leleh. Perhitungannya adalah sebagai berikut:
Hasilnya tidak sama tetapi lebih mendekati.
Lalu bagaimana dengan defleksinya, mas?
Banyak orang berpikir bahwa desain penampang balok (baik struktur baja maupun beton) hanya dipengaruhi oleh faktor kekuatan saja. Faktor daya layan (kenyamanan akibat defleksi yang memenuhi syarat) adalah hanya faktor pelengkap saja (banyak yang berpikir jika struktur sudah aman secara kekuatan, maka biasanya defleksinya pun juga pasti masuk). Sehingga terjadi orientasi optimalisasi desain struktur baja yang salah kaprah, yaitu mendesain struktur bangunan baja dengan patokan nilai stress ratio yang sangat mepet seperti 0.9999999. Tentu saja secara peraturan, nilai stres ratio sebesar 0.9999, bahkan 1 pun masih masuk dalam kategori aman. Tapi bagaimana dengan defleksinya?..
Secara perhitungan, stress ratio semepet ini (biasanya terjadi pada balok baja penampang kompak dengan bentang panjang dan disertai dengan kekangan lateral yang cukup baik sehingga balok baja akan mampu mencapai tahanan momen plastisnya) akan menghasilkan struktur yang bermasalah pada defleksinya. Alias perlu dicek defleksi yang terjadi dengan cermat.
Bagaimana dengan defleksi pada beton, mas?
Ini yang menarik. Perhitungan defleksi pada beton sebenarnya perlu memperhitungkan inersia efektif akibat retak beton. Pada Sap2000, jika kita tidak mereduksi properti kekakuan inersia suatu balok, maka defleksi yang dihasilkan pun tentu saja bisa menghasilkan angka yang tidak benar (tidak sesuai perhitungan seharusnya).
Pada peraturan SNI-03-2847-2002, Pasal 11.5.2(3)) telah diberikan rumus inersia efektif untuk menghitung lendutan. Rumusnya adalah sebagai berikut:
Nilai inersia inilah yang valid digunakan untuk mengecek lendutan balok beton. Mcr sudah pernah kita hitung di atas. Ma (Momen maksimum yang terjadi pada tengah bentang balok) juga sudah kita hitung. Yang belum adalah menghitung Icr (Inersia penampang retak). Berikut adalah perhitungannya:
Setelah nilai Icr didapatkan, maka nilai Ieff dapat kita peroleh. Berikut hasil perhitungannya (beban yang digunakan adalah beban layan):
Bandingkan dengan nilai Inersia penampang balok 300.400 tanpa retak:
Rasionya adalah sebesar: Ieff/Ig = 0.368
Sedangkan SNI telah memberikan nilai faktor reduksi retak ini pada Pasal 12.11.1. Untuk struktur balok, nilai faktor reduksi inersianya adalah sebesar 0.35. Nilainya ternyata mendekati nilai hasil perhitungan manual. Maka untuk mendapatkan nilai lendutan dengan memperhitungkan faktor retak beton ini, inersia penampang perlu direduksi sebesar 0.35 (mengikuti peraturan SNI). Nilai 0.35 ini memang cukup konservatif namun bisa dibilang adalah solusi yang sangat memudahkan. Untuk merubah inersia ini dapat dilakukan dengan meng-klik: “Define -> Frame Section -> B300.400 -> Modify/Show Property -> Set Modifiers”. Maka akan keluar window seperti berikut:
Ubah nilai “Moment of Inertia about 3 axis” menjadi 0.35.
Dengan perhitungan manual, maka besar defleksi maksimumnya adalah sebagai berikut:
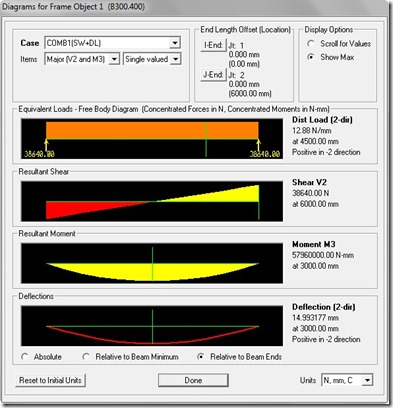
Sedangkan defleksi balok hasil Sap2000 adalah sebagai berikut:
Nilainya defleksi berbeda namun sangat mendekati. Hanya berbeda 0.0838 mm (lebih besar hasil perhitungan manual).
Sekian dulu untuk postingan kali ini dan terima kasih. CMIIW..
(Lihat juga tulisan “Verifikasi Penulangan Geser Balok Beton Sap2000” di sini.)