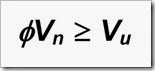Pada tulisan yang lalu kita sudah berhasil melakukan proses verifikasi output penulangan lentur balok Sap2000 dengan hitungan manual. Sekarang saatnya mencoba memverifikasi output penulangan geser/sengkang Sap2000. :-)
Banyak yang mengira bahwa tegangan geser yang terjadi pada penampang melintang suatu balok adalah sama besarnya di tiap titik penampang. Contohnya seperti berikut: Jika sebuah balok persegi berukuran b (lebar) x h (tinggi) = 300 mm x 400 mm diberi beban geser sebesar 100 kN, maka tegangan geser penampang yang kita peroleh menurut perhitungan sederhana adalah sebesar: 100 kN/ (300 mm x 400 mm) = 833.33 kN/m = 0.833 MPa.
Tapi apakah itu benar?
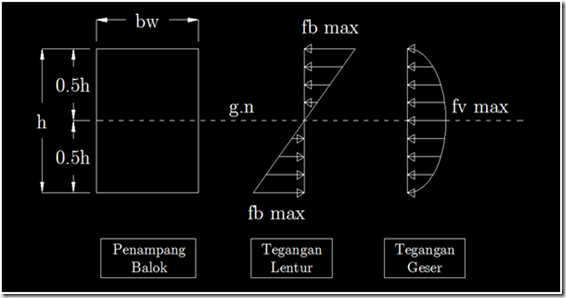
Tegangan geser sebesar 0.833 MPa ini sebenarnya adalah tegangan geser rata-rata, bukan tegangan geser aktual. Tegangan geser aktual (untuk balok penampang persegi ini) memiliki bentuk parabola dimana pada sumbu netral balok akan terjadi tegangan geser maksimum, sedangkan pada serat sisi terluar (baik sisi atas maupun bawah balok) akan terjadi tegangan geser minimum (0 MPa), alias tidak ada tegangan geser yang terjadi. Jika digambarkan, maka bentuk tegangan geser aktualnya adalah seperti gambar berikut:
Diagram tegangan geser diatas menunjukkan bahwa tegangan geser maksimum terjadi tepat pada tengah badan/web, ini menjawab pertanyaan kenapa retak geser dimulai pada daerah tengah balok, berbeda dengan retak lentur yg dimulai dari tepi balok. Untuk mengerti kenapa diagram gaya geser membentuk bentuk parabola semacam gambar di atas dapat dipelajari dengan memahami tegangan geser horizontal yg terjadi pada balok akibat beban lentur. Pemahaman tegangan geser horizontal akibat beban lentur ini juga penting untuk memahami perilaku struktur komposit.
Lalu bagaimana cara menghitung tegangan geser aktual tersebut? Untuk menghitung besarnya tegangan geser aktual suatu penampang dapat dihitung dengan rumus sederhana sebagai berikut:
Dimana: v = tegangan geser, V = gaya geser, Q = momen statis dari bagian penampang di atas potongan horizontal yang sedang ditinjau, I = momen inersia penampang, dan b = lebar penampang balok.
Sedangkan untuk mencari nilai tegangan geser maksimum dapat diketahui dengan memberikan nilai Q maksimum pada rumus di atas. Penurunan rumus tegangan geser maksimum dengan memasukkan nilai Q maksimum pada rumus tegangan geser di atas adalah sebagai berikut:
Nampak pada hasil penurunan rumus di atas, besarnya tegangan geser maksimum adalah sebesar 3/2 kali tegangan geser rata-rata. Bagaimana dengan tegangan geser yang dihitung oleh Sap2000? Apakah menggunakan tegangan geser rata2 atau tegangan geser aktual? Akan kita cari jawabannya di bawah.
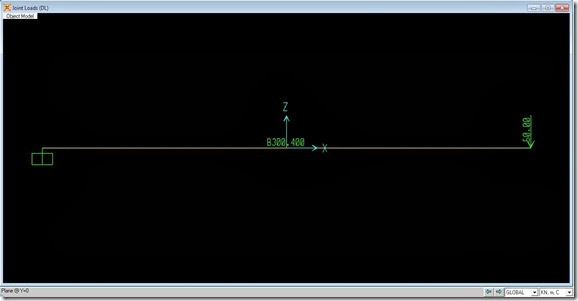
Sekarang mari kita mulai proses verifikasi penulangan geser balok Sap2000 dengan hitungan manual. Sebagai benda uji coba masih kita gunakan balok yg sama, yaitu balok B300.400 agar konsisten dengan hitungan pengecekan tulangan lentur di tulisan yang lalu. Perbedaannya di tulisan ini, saya merubah struktur balok menjadi struktur kantilever sepanjang 2 m. Sedangkan untuk properti bahan yang dipakai juga masih sama, yaitu: kuat tekan beton fc’ = 30 MPa, fy = 400 MPa (tegangan leleh tulangan lentur) , dan fys = 240 MPa (tegangan leleh tulangan sengkang). Bentuk permodelan pada Sap2000 dapat dilihat pada gambar di bawah:
Sebelum kita lanjut memberikan pembebanan yg “efektif” pada balok di atas, kita perlu menganalisis beban-beban kritis yg dapat memberikan petunjuk apakah Sap2000 benar-benar mengikuti aturan/syarat2 penulangan sesuai peraturan beton (SNI) atau tidak.
Pertama-tama kita perlu mengetahui variabel penentu kekuatan geser suatu balok beton. Berdasarkan SNI Beton (dan juga rumus umum yg kita dapatkan pada bangku kuliah), kekuatan geser beton ditentukan oleh dua hal, yaitu kekuatan geser beton itu sendiri dan ditambah dengan kuat geser dari tulangan geser (sengkang). Maka kuat geser nominal total suatu struktur balok bertulang dapat diekspresikan dengan rumus berikut:
Dimana: Vn = kuat geser nominal total, Vc = kuat geser nominal beton, Vs = kuat geser nominal sengkang.
Sedangkan untuk kuat geser ijin beton, rumus di atas perlu dikalikan dengan faktor reduksi untuk kuat geser sebesar ø = 0.75 (sesuai SNI 03-2847-2002 Pasal 11.3.(3)) dan nilainya minimal harus sama dengan atau lebih besar dari gaya geser ultimate yang terjadi:
Dari rumus di atas, rumus kuat geser beton (Vc) untuk struktur yang mengalami “gaya lentur dan geser saja” (tanpa gaya aksial) adalah sebagai berikut (sesuai SNI 03-2847-2002 Pasal 13.3.(2).1):
Dimana: fc’ = kuat tekan beton silinder umur 28 hari, bw = lebar balok, d = tinggi efektif balok.
Sedangkan untuk struktur kolom yang memikul beban aksial (tekan maupun tarik) yang cukup besar (lebih dari 0,1.fc’.Ag), rumus di atas kurang ideal karena tidak memperhitungkan pengaruh beban aksial terhadap kekuatan geser beton. Intinya adalah, gaya tekan akan menyebabkan kekuatan geser meningkat, sedangkan gaya tarik akan menyebabkan kekuatan geser menurun. Fenomena ini dapat kita pahami dengan cara menekan tumpukan uang logam seperti gambar di bawah dan memberinya beban geser:
Hasilnya, tumpukan logam yang diberi tekanan aksial akan lebih sulit untuk berdeformasi terhadap beban geser dibandingkan dengan tumpukan uang logam yang tanpa diberi beban aksial sama sekali.
Sedangkan untuk rumus kuat geser nominal sengkang (Vs) yang arahnya tegak lurus sumbu aksial (dipasang vertikal tanpa kemiringan) adalah sebagai berikut:
Dimana: Av = luas tulangan geser, fy = kuat leleh tulangan sengkang, d = tinggi efektif balok, dan s = jarak antar sengkang. Perhatikan bahwa rumus d/s adalah menunjukkan jumlah sengkang.
Bagaimana dengan pengaruh beban momen terhadap kekuatan geser?
Selain beban aksial tarik, momen lentur ternyata juga dapat mengurangi kemampuan balok dalam menahan geser. Kenapa? Hal ini terjadi karena faktor retak penampang beton (akibat beban lentur) yang dapat mengakibatkan luas efektif penampang geser menjadi berkurang. Maka untuk memperhitungkan kuat tahanan geser beton yang dipengaruhi oleh beban lentur ini dapat menggunakan rumus berikut (sesuai SNI 03-2847-2002 Pasal 13.3.(2).1):
Dimana: ρw = rasio luas tulangan terpasang, Vu = gaya geser ultimate, Mu = gaya momen ultimate, bw = lebar balok, d = tinggi efektif balok.
Namun nilai Vc di atas dibatasi tidak boleh lebih dari:
Dan persyaratan lainnya adalah:
Lalu, apakah Sap2000 memperhitungkan pengaruh dari gaya momen ini dalam menentukan kuat geser beton?.. Nanti akan kita cek juga.
Selain itu, seperti halnya tulangan lentur, tulangan geser juga memiliki nilai luasan tulangan maksimum dan minimum. Luas tulangan geser minimum dapat dicari dengan rumus berikut (sesuai SNI 03-2847-2002 Pasal 13.5.(5).3):
Dan nilai di atas dibatasi tidak boleh kurang dari:
Lalu, kapan luas tulangan geser minimum ini perlu dipasang pada balok? Berdasarkan peraturan (SNI 03-2847-2002 Pasal 13.5.(5).1) disebutkan bahwa luas tulangan geser minimum perlu diberikan jika gaya geser ultimate balok (Vu) melebihi nilai 0.5(øVc).
Dan selanjutnya yang penting untuk dipahami, penggunaan tulangan geser (Vs) memiliki batas, alias kita tidak bisa memasang tulangan geser sebanyak mungkin (tanpa hingga) pada suatu dimensi balok tertentu. Ada suatu kondisi dimana ketika nilai kuat geser sengkang yang terpasang melebihi nilai tulangan geser maksimum, maka dimensi balok perlu diperbesar. Menurut SNI 03-2847-2002 Pasal 13.5.(6).9, nilai kuat geser sengkang maksimum tersebut ditentukan dengan rumus berikut:
Karena nilai Vs maksimum sudah dapat kita tentukan (Vs maks = 2/3 √fc’ x bw x d), maka selanjutnya dapat kita peroleh rumus praktis untuk menentukan gaya geser ultimate yang dapat dipikul oleh balok berdimensi b x h. Penurunannya adalah sebagai berikut:
Ok, rumus-rumus penting untuk menghitung kuat geser beton bertulang sudah disampaikan di atas. Menariknya adalah Sap2000 menghasilkan output tulangan geser dalam bentuk satuan mm2/mm. Dengan kata lain, Sap2000 tidak mau ambil pusing untuk menentukan jarak spasi antar sengkang. Sedangkan kita perlu memberikan informasi penulangan sengkang pada hasil desain berupa: jumlah kaki sengkang, diameter sengkang, dan jarak antar sengkang yang biasa disimbolkan dalam bentuk: 2 Ø 10 – 150 mm (yang berarti diperlukan pemasangan sengkang dua kaki berdiameter 10 mm dengan jarak antar sengkang dari pusat ke pusat sebesar 150 mm).
Lalu bagaimana dong? Tenang, ini hal yang mudah. Di bawah akan saya tunjukkan bagaimana mentransformasi hasil output penulangan sengkang Sap2000 menjadi bentuk yang lazim kita kenal.
Terkait dengan batasan desain oleh peraturan SNI (pada program Sap2000 ini diwakili oleh peraturan ACI 388-99), berikut adalah pertanyaan2 yang akan dijawab pada proses verifikasi tulangan geser kali ini:
1 . Apakah Sap2000 memperhitungkan pengaruh momen lentur dalam menentukan kuat geser beton?
2 . Apakah Sap2000 akan memberikan tulangan geser untuk gaya geser yang kurang dari 0.5(øVc)?
3 . Apakah Sap2000 memberikan luas tulangan minimum untuk gaya geser > 0.5øVc?
4 . Apakah Sap2000 membatasi nilai tulangan geser maksimum sebesar 2/3 x √fc x bw x d? Dan apa yang dilakukan oleh Sap2000 ketika nilai Vs melebihi nilai maksimum ini?
Mari kita peroleh jawaban untuk pertanyaan 1:
Mula2, kita kenakan beban titik terpusat sebesar 50 kN sebagai beban mati pada ujung bentang balok. Beban mati sendiri balok akan saya abaikan (yaitu dengan memberikan nilai ”self weight multiplier = 0” pada load case bersangkutan).
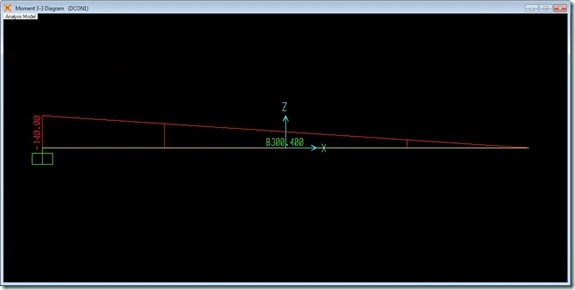
Sehingga reaksi gaya yang dihasilkan pada ujung bentang terkekang adalah sebesar: Mu = 1.4 x 50 kN x 2 m = 140 kN.m
Sedangkan dihasilkan nilai Vu adalah sebesar: Vu = 1.4 x 50 kN = 70 kN (merata sepanjang balok)
Oya, sebelum berjalan lebih jauh, pastikan faktor reduksi untuk kuat lentur dan kuat geser dalam Sap2000 disesuaikan dengan nilai faktor reduksi SNI Beton kita:
Dan jangan lupa juga untuk merubah tipe struktur menjadi “Sway Ordinary”, atau dalam bahasa SNI kita adalah sama dengan SRPMB (Sistem Rangka Pemikul Momen Biasa), karena secara default (program determined), Sap2000 akan menghitung struktur dengan sistem “Sway Special” / SRPMK (Sistem Rangka Pemikul Momen Khusus). Tentu saja perbedaan tipe sistem ini akan menyebabkan output penulangan yang berbeda juga.
Setelah melakukan proses analysis gaya dan desain penulangan, maka dihasilkan tulangan lentur balok seperti di bawah:
Dan dengan meng-klik kanan batang balok tersebut, dapat kita peroleh data yg lebih detail dari hasil proses analysis dan desain. Berikut adalah beberapa data yg dapat diperoleh dari penulangan lentur:
Dan berikut adalah beberapa data yg didapat dari penulangan geser:
Terlihat bahwa hasil perhitungan Sap2000 untuk kuat geser ijin beton B300.400 adalah sebesar 69.584 kN.
Sekarang mari kita bandingkan dengan perhitungan manual. Pada perhitungan manual ini, akan saya coba lakukan perhitungan 3 beban titik terpusat pada ujung bentang yang memiliki nilai berbeda (12 kN, 50 kN, dan 85 kN) untuk melihat pengaruhnya terhadap kuat geser beton. Perhitungannya adalah sebagai berikut:
Berdasarkan hasil kalkulasi di atas, dapat terlihat bahwa kuat geser beton yang dihasilkan oleh Sap2000 ternyata tidak memperhitungkan pengaruh dari adanya gaya momen (terlihat dari output nilai kuat geser ijin beton Sap2000 (øVc sap = 69.584 kN) lebih mendekati nilai kuat geser ijin beton hasil hitungan manual tanpa memperhitungkan gaya momen (øVc = 69.835 kN)).
Dan kesimpulan lainnya yang menarik adalah, dengan membandingkan kuat geser beton yang dihasilkan dari 3 beban yang berbeda (øVc rev), terlihat bahwa dengan semakin besarnya gaya momen yang timbul ternyata akan memperbesar nilai kuat geser beton. Menarik bukan. :-) Berdasarkan penjelasan dari buku, hal ini terjadi lebih disebabkan karena semakin kecilnya retak beton yang terjadi seiring banyaknya tulangan lentur yang terpasang akibat meningkatnya gaya momen.
Bagaimana dengan tegangan gesernya?
Kita sudah membahas tegangan geser pada pembukaan tulisan ini, walaupun nilai tegangan geser ini tidak ada pengaruhnya dalam perhitungan tulangan sengkang, tapi tidak ada salahnya jika kita memeriksan dan membandingkan dengan perhitungan manual.
Langsung saja, Sap2000 memberikan output nilai tegangan geser sebagai berikut:
Tegangan geser yang terjadi akibat beban Vu adalah sebesar 686.275 kN/m2, kapasitas tegangan geser beton = 682.199 kN/m2, dan tegangan geser maksimum yg dapat dipikul oleh balok beton bertulang berdimensi 300 mm x 400 mm adalah 4547.997 kN/m2.
Sedangkan berdasarkan perhitungan manual, tegangan geser yang didapatkan adalah sebagai berikut:
Berdasarkan hasil perhitungan di atas terlihat bahwa tegangan geser yang dihasilkan oleh Sap2000 (686.275 kN/m2) diperoleh dari rumus tegangan geser rata-rata, bukan rumus tegangan geser aktual.
Lanjut, kita jawab pertanyaan ke 2: Apakah Sap2000 akan memberikan tulangan geser untuk balok dengan gaya geser yang nilainya kurang dari 0.5(øVc)?
Pada perhitungan di atas, sudah kita dapatkan besarnya kuat geser ijin beton (øVc) sebesar 69.584 kN. Berdasarkan data tersebut dapat kita peroleh nilai 0.5(øVc) = 0.5 (69.584 kN) = 34.792 kN. Sehingga untuk mendapatkan jawaban dari pertanyaan di atas, nilai beban titik terpusat yang perlu diberikan pada struktur balok harus lebih kecil dari 34.792 kN / 1.4 = 24.851 kN. Pada permodelan Sap2000 akan kita berikan beban titik terpusat sebesar 23 kN ( < 24.851 kN)
Sehingga hasil desain tulangan gesernya adalah sebagai berikut:
Ya, terbukti Sap2000 tidak akan memberikan tulangan sengkang pada balok yang menerima gaya geser kurang dari 0.5(øVc).
Lanjut, kita jawab pertanyaan ke 3: Apakah Sap2000 akan memberikan tulangan geser minimum untuk gaya geser yang nilainya lebih besar dari 0.5(øVc)?
Untuk mendapatkan jawaban dari pertanyaan di atas, nilai beban titik terpusat yang perlu diberikan pada struktur balok harus lebih besar dari 24.851 kN. Selanjutnya, pada permodelan Sap2000 akan kita berikan beban titik terpusat sebesar 26 kN ( > 24.851 kN)
Berdasarkan beban di atas, maka diperoleh hasil penulangan geser sebagai berikut:
Sap2000 memberikan hasil ouput penulangan geser sebesar 0.431 mm2/mm. Sebentar, apakah nilai tulangan yang dihasilkan dalam satuan mm2/mm oleh Sap2000 di atas sama nilainya dengan luasan tulangan geser minimum sesuai rumus yang kita ketahui?.. Bagaimana cara mengeceknya jika satuannya mm2/mm begitu?
Mudah saja. Sebenarnya satuan mm2/mm didapatkan dari hasil pembagian antara luas tulangan geser yang dibutuhkan dengan spasi antar tulangan geser = Vs / s. Penurunan rumusnya adalah sebagai berikut (catatan: s = sp = spasi sengkang):
Maka berdasarkan kalkulasi manual, didapatkan nilai besar luas tulangan geser minimum dengan satuan mm2/mm adalah sebagai berikut:
Walaupun hasilnya sedikit berbeda, namun hasil kalkulasi di atas dapat membuktikan bahwa Sap2000 memang memberikan nilai tulangan geser minimum untuk gaya geser ultimate yang nilainya lebih besar dari 0.5(øVc). Tulangan geser minimum ini akan tetap konstan digunakan oleh Sap2000 selama gaya geser Vu belum melebihi nilai (øVc + øVs min).
Selanjutnya kita cek kuat geser ijin tulangan sengkang (øVs) minimum hasil output Sap2000 dengan perhitungan manual. Berdasarkan hasil perhitungan Sap2000, diperoleh nilai øVs sebagai berikut:
Sedangkan dengan hitungan manual (dengan menggunakan nilai Av/s hasil Sap2000 = 0.431 mm^2/mm), diperoleh nilai øVs sebagai berikut:
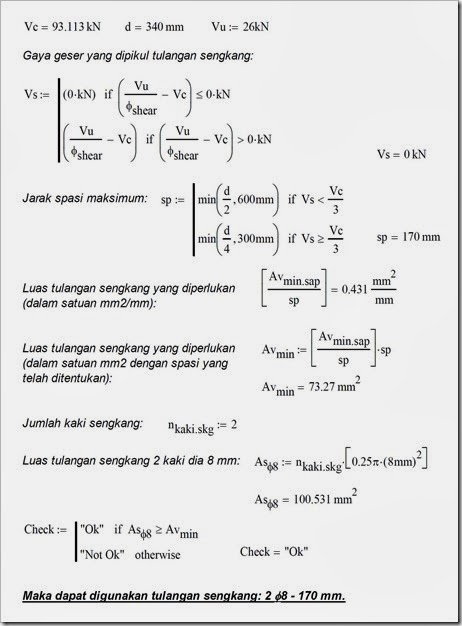
Lalu bagaimana cara mentransformasi hasil output penulangan geser Sap2000 di atas agar dapat dibaca dengan mudah oleh pekerja di lapangan? Caranya adalah sebagai berikut:
Cara di atas juga dapat dilakukan untuk nilai Vs > 0 kN.
Selanjutnya, kita jawab pertanyaan ke 4: Apakah Sap2000 membatasi nilai kuat tulangan geser maksimum sebesar 2/3 x √fc’ x bw x d? Dan apa yang dilakukan oleh Sap2000 ketika nilai Vs melebihi nilai maksimum ini?
Untuk menjawabnya, perlu kita cari besar beban geser maksimum yg akan menyebabkan kondisi ini. Gaya geser maksimum dapat kita peroleh dengan rumus Vu = 0.625 x (√fc’ x bw x d) (silahkan lihat ke atas kembali untuk mengetahui asal rumusnya). Maka, berdasarkan perhitungan manual, beban mati (DL) yang dapat menyebabkan balok di ambang kondisi geser maksimum adalah sebagai berikut:
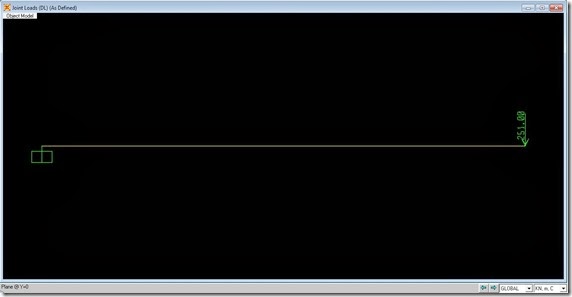
Berdasarkan data di atas, akan kita berikan beban titik terpusat sebesar 251 kN ( > 249.409 kN) pada balok permodelan Sap2000:
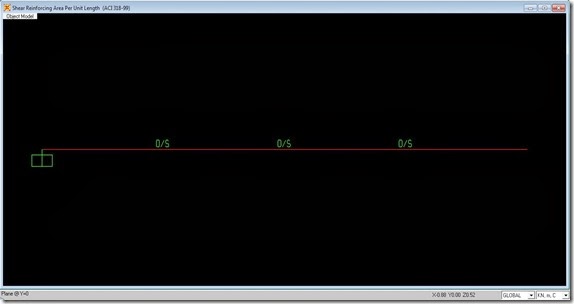
Berdasarkan beban di atas, maka diperoleh hasil penulangan geser sebagai berikut:
Hasilnya adalah Sap2000 akan memberikan warning/peringatan dengan simbol tulisan O/S = Over Stress. Dan terlihat juga Sap2000 sama sekali tidak menampilkan jumlah luas tulangan geser yang diperlukan (Rebar Area = 0 mm2). Bagaimana solusinya? Seperti yang sebelumnya telah disebutkan di atas, solusi yang paling efektif adalah dengan memperbesar dimensi balok.
Sekian untuk tulisan kali ini. Untuk tulisan selanjutnya akan kita coba verifikasi output penulangan torsi balok. Seperti kita ketahui, output penulangan torsi akan menghasilkan output berupa tulangan lentur dan tulangan geser. Sap2000 menyajikan tiap tulangan ini secara terpisah. Yang menjadi pertanyaan, apakah hasil ketiga tulangan ini dijumlahkan atau diambil yang terbesar? Tunggu tulisan selanjutnya.. :-) Semoga berguna.. CMIIW..