Wah, sudah lama sekali saya tidak membuat lanjutan tulisan yang berjudul Ngulik Sap2000 Part 1. Maaf jika ada yang menunggu.. <:-) Mohon maklum ya. :-) Akhirnya muncul juga lanjutannya.. Semoga berguna. :-)
Yuks, langsung saja mas?
Yuk mare.. :-)
Sudah kita ketahui pada tulisan sebelumnya (Part 1), nilai kuat lentur balok (dengan panjang terkekang lateral yang cukup tanpa menimbulkan masalah terhadap tekuk torsi lateral) dipengaruhi oleh dua nilai bentuk penampang, yaitu nilai modulus elastis penampangnya (S) dan nilai modulus plastis penampangnya (Z), dimana penurunan rumus modulus elastis penampang dan kaitannya dengan nilai tahanan momen maksimum sudah kita bahas bersama di Part 1.
Yang menarik dari modulus plastis ini adalah adanya kata “plastis”. Secara refleks kita akan berpikir; “Loh, kok boleh sampai kondisi plastis? Kalau sudah mencapai kondisi plastis bukankah berarti nilai fy (tegangan leleh) sudah terlampaui dan artinya bukankah rumus dengan analisis linear sudah tidak valid lagi untuk digunakan?”..
Pertanyaan yang lumrah, karena selama ini kita selalu mematok nilai fy (batas tegangan elastis) sebagai batas atas tegangan penampang. Kenapa? Karena rumus2 yang biasa kita gunakan untuk menghitung regangan dan tegangan penampang memiliki karakteristik yang linear, alias hubungan tegangan dan regangan masih memiliki rasio (σ/ε) yang tetap. Berbeda jika terjadi kondisi plastis, kita tidak bisa mencari besarnya tegangan suatu penampang berdasarkan besarnya regangan (maupun sebaliknya) dari rumus linear yang selama ini kita gunakan.
Jika kita mengamati diagram tegangan sebuah penampang balok sederhana yang mengalami reaksi momen akibat pembebanan dimana serat tepi atas dan tepi bawah tepat mengalami tegangan leleh seperti di bawah:
kita akan melihat ada bagian serat penampang balok yang belum mengalami leleh, yaitu pada area bagian tepi bawah serat tarik dan pada area bagian tepi atas serat tekan. Semakin ke tengah, tegangan akan semakin kecil secara linear dan tepat pada garis netral tegangan akan bernilai = 0. Bagian yang belum mengalami leleh ini sebenarnya memiliki tahanan terhadap momen hingga tegangan leleh tercapai. Namun untuk penampang yang dikategorikan “tidak kompak”, kontribusi area ini dalam menahan momen hingga kondisi leleh sengaja untuk diabaikan (tidak diperhitungkan) karena faktor stabilitas bagian penampang yang mengalami gaya tekan. Pada penampang balok yang dikategorikan “kompak”, kekuatan di area ini dapat dikerahkan hingga seluruh area mencapai kondisi leleh tanpa terjadinya gangguan stabilitas pada daerah tekan penampang, sehingga hasilnya penampang kompak pun akan memiliki tahanan momen yang lebih besar daripada penampang tidak kompak.
Lalu bagaimana dengan area yang sudah mengalami kondisi plastis?
Jika kita melihat grafik tegangan-regangan material baja seperti di bawah:
Terlihat bahwa deformasi yang terjadi setelah baja mengalami tegangan leleh tidak merubah besarnya tegangan hingga pada titik batas regangan tertentu (titik regangan batas deformasi plastis dan “daerah pengerasan” (atau istilah kerennya: strain hardening)). Dengan kata lain, walaupun kondisi leleh sudah terjadi pada serat paling luar penampang, penampang yang kompak dianggap mampu terus mengembangkan deformasi hingga semua serat penampang mengalami kondisi leleh tanpa mengakibatkan peningkatan tegangan.
Bagaimana dengan rumus modulus plastis penampangnya?
Di beberapa buku yang pernah saya baca, saya amati banyak yang tidak menjelaskan penurunan rumus modulus plastis penampang (secara mudah). Ujug-ujug biasanya langsung ditampilkan rumus modulus plastis penampang balok IWF untuk arah sumbu kuat seperti di bawah:
Zx = (b.tf)(h - tf) + tw(1/2h – tf)(1/2h - tf)
Dimana:
tf = tebal flange, tw = tebal web, h = tinggi profil, b = lebar profil
Jika melihat rumus di atas, mungkin kita akan berpikir lebih lama untuk mencari tahu bagaimana rumus itu bisa diturunkan. Namun untuk penampang balok persegi, rumusnya terlihat lebih sederhana, yaitu seperti berikut:
Zx = 1/4. b. h2
Rumus opo tho kui, mas? Seko endi asale?
Seebenarnya cukup mudah untuk memahami proses penurunan bentuk rumus di atas. Sebelum meninjau penurunan rumus (secara sederhana) dari modulus plastis penampang, agar bisa lebih memahami konsepnya, kita mulai saja dulu memahami penurunan rumus modulus elastis penampang untuk balok pejal sederhana. Di tulisan Ngulik Sap2000 Part 1, kita sudah mencoba mencari korelasi antara modulus elastis penampang dari nilai momen inersia penampangnya. Namun untuk rumus modulus plastis penampang sudah tidak ada korelasinya lagi dengan momen inersia penampang. Sehingga kedua nilai modulus penampang ini akan kita turunkan dari analisa diagram tegangannya.
Untuk mempermudah pemahaman, saya akan menggunakan penampang balok pejal sederhana sebagai bahan analisa. Berikut adalah diagram tegangan dari penampang balok pejal sederhana:
Dimana: C = Compression (Tekanan), T = Tension (Tarikan)
Karena penampang berbentuk simetris, maka nilai C dan T adalah sama. Nilai C dan T ini diperoleh dengan cara mengalikan tegangan leleh dengan luas penampangnya. Sehingga diperoleh rumus resultan gaya tekan C = 1/2.fy.B.(1/2.H). Jika disederhanakan menjadi:
C = (1/4.B.H).fy
Dari nilai C ini dapat kita cari tahanan momen elastisnya dengan cara mengalikan nilai C dengan lengan momennya (jarak antara gaya C dan T) sebesar 2/3.H. Sehingga:
Mn = C.(L momen)
Mn = (1/4.B.H).fy.(2/3.H)
Mn = (1/6.B.H2).fy
Sebelumnya sudah kita ketahui bahwa:
Mn = Sx .fy, maka
Sx = 1/6.B.H2 ==> Cocok.
Ini penurunan untuk rumus modulus penampang elastis. Untuk penurunan rumus modulus penampang plastis, kita menggunakan diagram tegangan seperti berikut:
Dari gambar di atas dapat diperoleh rumus resultan gaya tekan sebagai berikut:
C = 1/2.(B.H).fy
Dari nilai C ini dapat kita cari tahanan momen plastisnya dengan cara mengalikannya dengan lengan momen (jarak antara gaya C dan T) sebesar 1/2.H. Sehingga:
Mnp =C.(L momen)
Mnp = 1/2.(B.H).fy.(1/2.H)
Mnp = (1/4.B.H2).fy
Dari rumus yang kita ketahui, dapat kita peroleh:
Mnp = Zx .fy, maka nilai modulus penampang plastisnya adalah
Zx = 1/4.B.H2
Mudah sekali, bukan? Konsep penurunan rumus modulus plastis penampang ini berlaku juga untuk bentuk-bentuk yang lain, termasuk untuk profil baja IWF. Berikut adalah contoh proses penurunannya:
Untuk mempermudah pemahaman, kita analisa bagian flange dan web secara terpisah. Untuk bagian flange, diagram tegangan dan rumusnya adalah sebagai berikut:
Dari gambar di atas dapat diperoleh rumus resultan gaya tekan sebagai berikut:
C1 = (B.tf).fy
Dari nilai C1 ini dapat kita cari tahanan momen plastis (untuk bagian flange) dengan cara mengalikan nilai C1 dengan lengan momen tegangan flange (jarak antara gaya C1 dan T1) sebesar (H – tf). Sehingga:
Mnp1 = C1.(L momen)
Mnp1 = (B.tf).fy.(H - tf)
Dan untuk bagian web, diagram tegangan dan rumusnya adalah sebagai berikut:
Dari gambar di atas dapat diperoleh rumus resultan gaya tekan sebagai berikut:
C2 = tw.(1/2.H-tf).fy
Dari nilai C2 ini dapat kita cari tahanan momen plastis (untuk bagian web) dengan cara mengalikan nilai C2 dengan lengan momen tegangan web (jarak antara gaya C2 dan T2) sebesar (1/2.H – tf). Sehingga:
Mnp2 = C2.(L momen)
Mnp2 = tw.(1/2.H-tf).fy.(1/2.H-tf)
Maka tahanan momen plastis totalnya adalah:
Mnp = Mnp1 + Mnp2
Mnp = (B.tf).fy.(H-tf) + tw.(1/2.H-tf).fy.(1/2.H-tf)
Mnp = [(B.tf)(H-tf) + tw.(1/2.H-tf).(1/2.H-tf)].fy
Sehingga,
Zx = (B.tf)(H-tf) + tw.(1/2.H-tf).(1/2.H-tf) ==> Cocok.
Wah, mudah sekali ya?
Yup, memang sangat mudah dipahami jika prosesnya diperlihatkan secara bertahap.
Sekarang kita cek hasil perhitungan rumus secara manual dengan nilai yang dihitung oleh Sap2000. Berdasarkan rumus, nilai modulus plastis penampang untuk profil IWF 400.200.8.13 adalah sebagai berikut:
Sedangkan jika kita cek pada Sap2000 nilai modulus plastisnya adalah:
Kesimpulan: Cocok.
Oke mas, nilai modulus plastisnya udah cocok. Trus, gimana dengan tahanan momen profil bajanya berdasarkan nilai modulus penampang ini?
Sebelumnya, kita abaikan dulu masalah torsi lateral dengan cara menetapkan bentang balok yang pendek. (Masalah tekuk torsi lateral ini akan dibahas pada Ngulik Sap2000 Part III) Untuk menentukan panjang bentang balok maksimum agar terhindar dari bahaya tekuk torsi lateral, kita gunakan rumus sederhana seperti berikut:
Lp = 790.ry / √fy
Maka didapat hasil panjang maksimal bentang balok terkekang lateral di ujung2nya agar terhindar dari analisa tekuk torsi lateral adalah sebagai berikut:
Untuk itu dalam permodelan digunakan beam dengan bentang 2 m (< Lp = 2.347 m).
Pertama-tama kita cek terlebih dahulu persyaratan kompak dan non-kompak penampang profil baja IWF (hati-hati, beda penampang maka nilai batasnya juga berbeda). Karena bagian profil IWF yang mengalami tekan ada dua bagian, yaitu bagian flange dan bagian web (sehingga ada dua macam tekuk lokal, yaitu tekuk lokal web dan tekuk lokal flange), maka syarat kompak dan non-kompak dicek terhadap kedua bagian ini.
Masing2 bagian memiliki nilai batas kelangsingannya masing-masing, yaitu:
1. Untuk pelat sayap (flange):
Kelangsingan penampang sayap: λf = B / (2.tf)
Syarat batas kompak / tidak kompak penampang sayap:
λp.f = 170 / √fy
λr.f = 370√(fy – fr)
dimana:
B = lebar profil, tf = tebal flange
fy = tegangan leleh (Untuk baja A36 / SS400, fy = 240 Mpa)
fr = tegangan sisa (biasanya diambil sebesar 70 Mpa, namun program Sap2000 tidak memperhitungkan nilai fr, alias fr = 0)
2. Untuk pelat badan (web):
Kelangsingan penampang web: λw = H / tw
Syarat batas kompak / tidak kompak penampang web:
λp.w = 1680 / √fy
λr.w = 2550 / √fy
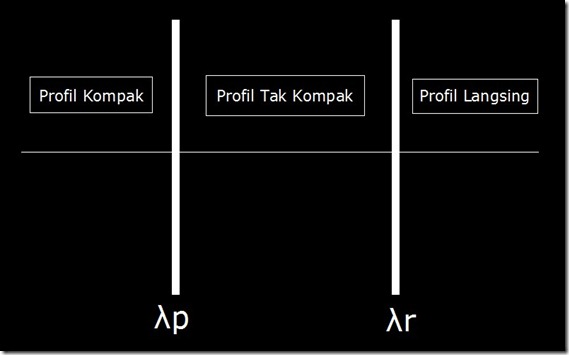
Profil termasuk kompak atau tidak kompak, aturannya adalah sebagai berikut:
Sekarang kita cek penampang profil WF400.200.8.13 secara manual:
Cek bagian flange:
Cek bagian web:
Penampang IWF400.200.8.13 secara perhitungan manual termasuk penampang kompak. Sehingga kuat ijin tahanan momen profil berdasarkan rumus adalah:
Dan berdasarkan hasil output sap2000, profil WF400.200.13.28 dengan bentang 2 m (tumpuan sendi-rol) memiliki tahanan ijin momen sebesar:
Kesimpulan: Cocok.
Sekian untuk Part II. CMIIW..















15 komentar:
om pande, pada bagian kompak Kelangsingan penampang sayap: λf = B / (2.tf), tetapi pada SNI 03-1729-2002 tabel 7.5.1. kelangsingan penampang sayap itu : λf = B / tf. Ada perbedaan, saya boleh tahu referensi rumus ini, terima kasih
whitecloud, sebenarnya sama saja. "B" yang saya ambil sama dengan lebar total profil WF. Sedangkan di SNI, "b" (dalam huruf kecil) yg diambil adalah setengah dari lebar profil WF. Perhatikan kalimat yg berbunyi: "(fy dinyatakan dalam MPa, simbol mengacu pada gambar 7.5.1)". Silahkan lihat gambar 7.5.1 untuk lebih jelasnya. Btw, terima kasih atas pertanyaannya.
terima kasih om atas infonya, Om pande sudah coba sap2000 versi 14 atau keatasnya om? pada define material steel sekarang ada fy efektif dan fu efektif ya tidak seperti versi sebelumnya, padahal di daftar baja tidak pernah dicantumkan nilai efektif ini. Kalo pengalaman om pande bagaimana mengisi fy dan fu efektif ini?
fy dan fu effective juga sudah ada pada sap versi 14 ke bawah. contohnya saya menggunakan sap versi 11 juga sudah ada. tapi tepatnya kapan sap2000 mulai memasukkan parameter ini saya tidak tahu secara pasti. Dengar2 ini berkaitan dengan adanya peraturan yg menggunakan nilai ini dalam perhitungan (CAN/CSA-S16-01). jadi, simpelnya, kalau kita tidak menggunakan peraturan ini ya diabaikan saja.
Sedangkan Sap2000 sendiri menerangkan parameter tersebut sebagai berikut:
"Expected yield (Fye) and expected tensile (Fue) stresses are the product of a code-prescribed factor and the expected strength of the material. This factor is typically around 1.1, as with FEMA 356 Table 5-3. These effective stress values represent the material response which occurs approximately halfway along the x-axis of the force-deformation relationship. FEMA 356 recommends using effective strength for deformation-controlled actions. Minimum strength represents the lower bound of nonlinear material response, which is best for force-controlled actions. Expected stress values are used to automatically generate hinge properties for P-M2-M3 and P-M hinges."
Silahkan diartikan sendiri. :-)
Ooh gitu ya om, jadi gak ada pengaruh dihasil akhirnya ya om, sebab saya baru balik lagi pakai sap2000 setelah lama gak pakai, karna tuntutan kerjaan aja. Biasa pakai etabs dan staad pro, sebab di sana tidak ada ini, bahkan etabs yang satu perusahaan juga tidak ada
iya, menurut saya sih begitu.. ingat, menurut saya lhoo.. he2.. silahkan kroscek sendiri lebih jauh ya.. :-)
Pak Pande,
Hasil Desain bapak di atas antara Manual dan Hasil Sap adalah sama untuk kasus balok di atas 2 tumpuan dengan perletakan sendi rol.
1.Apakah untuk Strutkur portal statis tertentu akan sama pak hasil pengecekan secara manual dengan Sap 2000? Berhubung saya mendapatkan kasus yang seperti ini. Yaitu hasil Sap 2000 agak sedikit yaoit di manual Momen hasil desain=1127.852 Kgm dan Sap = 11798,322 Kgm.
2. Kok di tabel baja jauh lebih rendah nilai Zx dari pada Sap dan rumus yang punya pak pande yang sama dengan Sap.
Zeth Rumahtita:
1. Kekuatan penampang tidak tergantung / tidak dipengaruhi dari apakah suatu struktur itu statis tertentu atau statis tak tentu. Jenis struktur tersebut (apakah statis tertentu atau statis tak tentu) hanya berpengaruh terhadap analisa gaya dalam yang diperoleh.
2. Tabel baja mana ya? Saya pakai data tabel baja PT.Gunung Garuda.
Terima kasih atas pertanyaannya.
Perkenalkan, saya dari tim kumpulbagi. Saya ingin tau, apakah kiranya anda berencana untuk mengoleksi files menggunakan hosting yang baru?
Jika ya, silahkan kunjungi website ini www.kumpulbagi.com untuk info selengkapnya.
Di sana anda bisa dengan bebas share dan mendowload foto-foto keluarga dan trip, music, video, filem dll dalam jumlah dan waktu yang tidak terbatas, setelah registrasi terlebih dahulu. Gratis :)
terimakasih banyak atas penjelasannya Om, kalau boleh saya mau bertanya bagaimana langkah-langkah untuk menghitung tegangan regangan yang terjadi pada balok baja menggunakan SAP2000
terimakasih banyak atas penjelasannya...
kalau boleh saya mau bertanya bagaimana langkah-langkah menghitung tegangan regangan pada balok baja menggunakan SAP 2000
permisi pak made , mw bertanya kalo analisa tegangan pada rectangel tube apakah sama caranya dengan I beam ?
saya mau bertanya jika kita menggunakan profil C kanal, tw apakah sama dengan d? dan tf sama dengan apa? mohon bantuannya:) saya sedang mengerjakan tugas besar:)
Mas cara membuat hinge gmn, n gmn dasar2 penentuan nilai hinge
makasih om, bermanfaat sekali
Posting Komentar